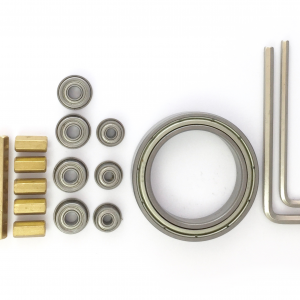6 Achs Knickarm Roboter Bausatz R-B
Der Miniatur Roboter für den Maker
Dieser 6 Achs Knickarmroboter folgt dem kinematischen Aufbau eines Industrieroboters. Im Gegensatz zu dem Roboterarm Modell mp-robot-a (mp-robot-kit) werden bei diesem Roboterarm alle sechs Achsen (0-5) mittels DOMAN S2000MD/S2003MD Servos angetrieben. Die stärkeren Servos im Handgelenk ermöglichen es auch größere Lasten in beliebiger Pose zu bewegen. Die S2000MD Servos weisen einen Drehbereich von ca. 180° auf. Der im Set enthaltene S2003MD Servo mit einem Drehbereich von 270° kann je nach benötigtem Arbeitsbereich des Roboters an der entsprechenden Achse verbaut werden. Die Nutzlast des Roboters liegt in etwa bei 300g bzw. 2.1Nm am Handgelenk. Der Bausatz besteht aus 20 gestanzten und gekanteten Blechteilen, 6 Servos, 7 Kugellagern und Schrauben + Muttern.
Die Montagewerkzeuge Inbusschlüssel, Maulschlüssel sind ebenfalls im Set enthalten. Die Ansteuerung des Roboters kann durch Steuerung der einzelnen Achsen, beispielsweise mit Hilfe eine Arduinos/Genuino oder Teensy Mikrocontrollers, realisiert werden. Weiter unten auf dieser Seite findest Du unsere Implementierung der Steuerung.
Dieser Roboterarm ist nicht für den industriellen Einsatz bestimmt. Der Roboter darf nur unter Aufsicht betrieben werden und ist hinsichtlich Absolut- und Wiederholgenauigkeit limitiert.

Technische Daten
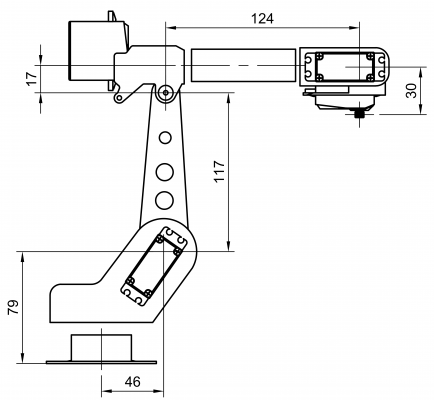
| Abmessungen | 18cm, 13cm, 23cm (HxBxT) |
| Reichweite | 30cm weit, hoch |
| Masse | 860g |
| DOMAN S2000MD |
|
| DOMAN S2003MD |
|
| Inhalt |
21 gestanzt und gekantete Blechteile |
7 Kugellager |
5 Servos DOMAN S2000MD |
1 Servos DOMAN S2003MD |
diverse Metallteile |
Schrauben und Muttern |
Maul- (5,5mm) und Inbusschlüssel |
Steuerung nicht Teil des Lieferumfanges (siehe unten) |
Die Videos zeigen Anwendungsbeispiele, die unter Umständen weitere Soft- und Hardwarekomponenten erfordern.
Downloads
Informationen
Arduino / Teensy 3.2 basierte Steuerung - Basiswissen
Zunächst ein paar Grundlagen zur Servosteuerung und Robotik. Wenn Du auf der Suche nach einer Steuerung bist, kannst Du dir auf GitHub unsere Implementierung ansehen. Die Todo-Liste hat auch noch ein paar Einträge, gerne merge ich deine Verbesserungen. :D - Max
Wahl des Mikrocontrollers
Zur Steuerung der Roboterachsen wird ein PWM (Pulsweiten Modulation) Signal benötigt (genaueres im Abschnitt Servomotoren). Grundsätzlich kann zur Steuerung des Roboters also jede Elektronik verwendet werden, die PWM Signale in entsprechender Frequenz und Länge erzeugen kann. Ein Arduino Uno verfügt bereits über 6 PWM Ausgänge (gekennzeichnet mit einer Tilde ~). Auch ein RaspberryPi verfügt über PWM Pins, die theoretisch zur Steuerung der Servomotoren verwendet werden können. Zuden gibt es auch PWM Platinen, mit denen bis zu 12 PWM Ausgänge mittels i2c oder SPI angesteuert werden können (z.B. Adafruit 16-Channel 12-bit PWM/Servo Driver).
Der Teensy ist ein größtenteils Arduino kompatibler, jedoch mit mehr Speicher (Arbeits+Programmspeicher) , schnellerem Prozessor, mehr Ausgängen und besserer USB Kommunikation ausgestatteter Microkontroller. Ich (Max) habe den Teensy 3.2 im Einsatz, da der Arduino schlicht nicht genug Programmspeicher für meine Implementierung der Steuerung aufweist. Und ein schnellerer Prozessor ist nie verkehrt :)
Motoren ansteuern
Die Achsen des Roboters werden mittels Servomotoren angetrieben. Die Arduino Servo Bibliothek bietet eine einfache API und eignet sich desshalb sehr gut für einfache Steuerungen.
#include <Servo.h>
Servo servo0; // Achse 0
Servo servo1; // Achse 2
[...]
void setup() {
servo0.attach(9); // Servo 0 nutzt Arduino Pin 9
servo0.attach(10); // Servo 1 nutzt Arduino Pin 10
servo0.write(45); // Servo zu 45° bewegen
}Wie unten im Abschnitt Servomotoren angesprochen, ist es sinnvoll, die Motoren zu kalibrieren. Die Ansteuerung
kann dazu einfach um das Ergebnis der Kalibrieung erweitert werden pulse = map(angle, 0, 180, 530, 2046);
(530us Pulsweite bei 0°, 2046 bei 180°). Der Servo wird nun mit servo0.writeMicroseconds(pulse) angesteuert.
[...]
void setup() {
[...]
int angle = 45;
pulse = map(angle, 0, 180, 530, 2046);
servo0.writeMicroseconds(pulse); // Servo zu 45° bewegen
}Geschwindigkeit
Hobby-Servomotoren fahren stets mit ihrer Maximalgeschwindigkeit die vorgegebene Zielposition an. Um den Motor dennoch mit variabler Geschwindikeit bewegen zu können, wird die Bewegung bis zur Zielposition in viele zeitlich gesteuerte Teilbewegungen aufgeteilt. Durch die vielen inkrementellen Bewegungen kann der Servo mit beliebiger Geschwindigkeit verfahren werden. Je kleiner das Positionsintervall, desto flüssiger ist die Bewegung.
int fromF = 1200; // Startfrequenz
int toF = 2000; // Zielfrequenz
int step = 2; // Schrittgröße
float v = 20 * 0.36; // Winkelgeschwindigkeit °/s
for (size_t i = fromF; i <= toF; i += step) {
servo0.writeMicroseconds(i);
delayMicroseconds(step / v * 1e6); // t = s/v
}Da die geschwindikeitsvariable Ansteuerung eine üblche Anforderung ist, stellen wir die Klasse VarSpeedServo auf GitHub zur Verfügung. Die Klasse bietet ein Interface, mit dem kalibrierte Servos in beliebiger Geschwindigkeit verfahren werden können. Hier ein Beispiel:
// pin, Maximalgeschwindigkeit, min. Pulsweite, max PW.m min. Winkel, max. Winkel, Homeposition
VarSpeedServo servo0(9, vel, 545, 1970, -90 * DEG_TO_RAD, 90 * DEG_TO_RAD, 0 * DEG_TO_RAD);
servo0.setTargetRadAngle(30*DEG_TO_RAD);
while(!servo0.atTargetAngle()){
servo0.process(20); // übergebe Intervall
delay(20);
}Inverse Kinematik - Steuerung mittels Koordinaten
Theorie
Üblicherweise werden programmierbare Bewegunsautomaten zur Manipulation von Objekten im Raum verwendet. Dafür muss der Roboter geometrisch definierte Posen (Position + Richtung) anfahren können. Die Inverse Kinematik (IK) beschäftigt sich mit der Fragestellung, Achswinkel zu finden, welche den Tool-Center-Point (TCP) des Roboters in eine vorgegebene Pose bringen. Dafür werden als Eingansparameter Pose, Konfiguration und Robotergeometrie eingegeben und entsprechende Achwinkel ausgegeben. Die sog. Konfiguration ist notwendig, da die Abbildung von Posen auf Achswinkel nicht eindeutig ist. Eine Pose kann unter Umständen durch mehrere Achswinkel erreicht werden (Ellbogen oben, unten; Basis um 180° gedreht). Die Konfiguration legt fest, in welchem Winkelbereich sich die einzelnen Achsen befinden sollen.
Grundsätzlich ist eine Inverse Kinematik umso komplexer, je mehr Freiheitsgrade ein System aufweist. Die IK eines Sechsachs-Knickarmroboters mit 6 Freiheitsgraden (Degreed of Freedom DOF) kann, bei geschickter Anordung der Achsen (Achse 3,4 (0-5) schneiden sich), mit algebraischen oder geometrischen Methoden vollständig bestimmt werden. Ein sieben achsiger Roboter (z.B. LBR IIWA) weist ohne Nebenbedingungen zu viele Freiheitsgrade auf, was eine geometrische und algebraische Lösung unmöglicht macht (Analogie menschlicher Arm: Man kann ein Objekt greifen und dennoch den Ellbogen bewegen -> unendlich viele Möglichkeiten). Mit numerischen Lösungsverfahren können auch Lösungen für überbestimmte Kinematiken gefunden werden.
Komplexe Trajektoren-Planer industriell eingesetzter Roboter berücksichtigen zudem meist Impulse und Achsmomente.
Praxis
Die Implementierung der Kinematik-Klasse in unserem GitHub Repository verfolgt den geometrischen Ansatz. Dieser erschien mir einfacher nachzuvollziehen und zu implementieren.
Beim geometrischen Ansatz werden die Achswinkel mit Hilfe von trigonometrischen Zusammenhängen ermittelt, indem die Gesamtkinematik in zweidimensionale Teilprobleme zerlegt wird. Folgend eine kleine Einführung in den geometrischen Ansatz. Die Kinematische Struktur des Roboters ist in folgender Abbildung dargestellt.
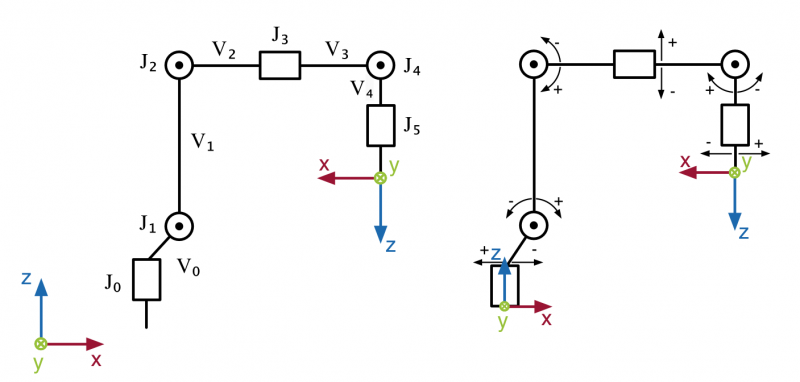
Der Punkt J4 wird bestimmt, indem die Pose um die Länge V4 in negative Z-Richtung des TCP-Koordinatensystems verschoben wird.
Die Gelenke J1-J4 können nun in der Ebene betrachtet werden, da keines eine Bewegung aus der Ebene hinaus ermöglicht. Die Längen V3 und V4 ergeben in Summe a. Durch Anwendung des Kosinussatztes können schließlich die Winkel α, β und γ berechnet werden.
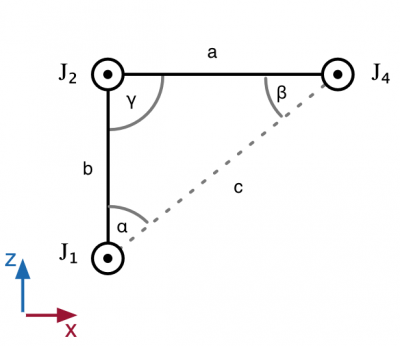
J1 kann aus der Summe von γ und δ berechnet werden.
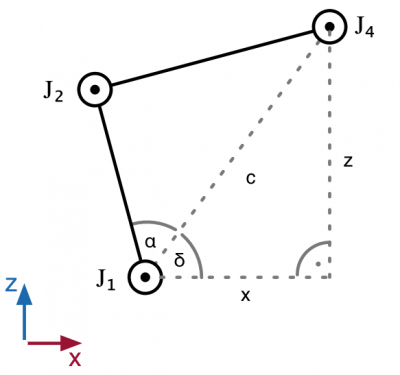
Die Berechnung von J3, J4 und J5 erfordert zudem Vektorrechnung, da es sich hierbei um ein 3-dimensinales Problem handelt.
Verknüpfte Kinematiken
Einige Roboter weisen zudem Kinematiken auf, bei denen Gelenke über Stangen bewegt werden. Das Gelenk J1 des Roboterarms in der Abbildung unten wird durch Bewegen der Stange h1 angesteuert. Die Position der Stange h1 beeinflusst dabei über die Verbindungsstange h2 die Stellung von J2. Sind die Strecken V1/h2 und h1/h3 gleich lang, so sind bedingt durch die Eigenschaften des Parallelogramms auch die Winkel alpha identisch.
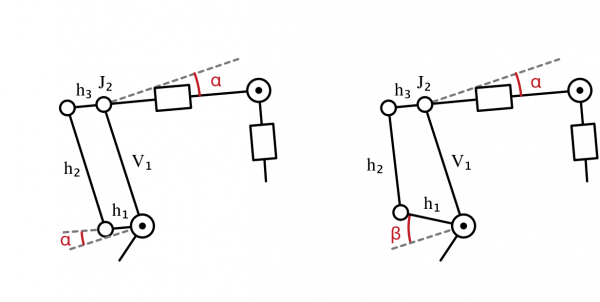
Weisen diese jedoch verschiedene Längen auf, so kann die geforderte Stellung alpha wie folgt berechnet werden.
float beta = 37 * DEG_TO_RAD;
float v_1 = 10;
float h_1 = 9;
float h_2 = 8;
float h_3 = 7;
// beta to alpha
float beta_ = (PI / 2 - beta);
float diag_1 = sqrt(v_1 * v_1 - 2 * v_1 * h_1 * cos(beta_) + h_1 * h_1);
float alpha_1 = acos((-h_2 * h_2 + h_3 * h_3 + diag_1 * diag_1) / (2 * h_3 * diag_1));
float alpha_2 = acos((-h_1 * h_1 + v_1 * v_1 + diag_1 * diag_1) / (2 * v_1 * diag_1));
float alpha = alpha_1 + alpha_2 - PI / 2;
std::cout << (alpha * RAD_TO_DEG) << '\n';
// alpha to beta
float alpha_ = alpha + PI / 2;
float diag_2 = sqrt(v_1 * v_1 - 2 * v_1 * h_3 * cos(alpha_) + h_3 * h_3);
float beta_1 = acos((-h_2 * h_2 + h_1 * h_1 + diag_2 * diag_2) / (2 * h_1 * diag_2));
float beta_2 = acos((-h_3 * h_3 + v_1 * v_1 + diag_2 * diag_2) / (2 * v_1 * diag_2));
beta = PI / 2 - (beta_1 + beta_2);
std::cout << (beta * RAD_TO_DEG) << '\n';
Kinematik Bibliothek
Zur Berechnung von vorwärts- und inverser Kinematik, stellen wir eine Bibliothek auf GitHub bereit. Zur Instanziierung der Klasse wird die Geometrie des Roboters übergeben. Die Geometriebeschreibung muss in einem zwei-dimensionalen Array in der oben gezeigten Koordinatenkonvention vorliegen.
float geometry[5][3] = { // Beispiel für micropede-robot-a
{ 5, 0, 7.3 },
{ 0, 0, 13.0 },
{ 1, 0, 2 },
{ 12.6, 0, 0 },
{ 0, 0, -3.6 }
};
Kinematic K(geometry)
float angles[6];
K->inverse(X, Y, Z, A, B, C, angles); // Euler X->Y->Z mitbewegte Achsen
std::cout << angles[0] << '\n';
std::cout << angles[1] << '\n';Analog dazu die Vorwärtskinematik.
float pose[6];
K->forward(90 * DEG_TO_RAD,
45 * DEG_TO_RAD,
0 * DEG_TO_RAD,
0 * DEG_TO_RAD,
180 * DEG_TO_RAD, // Z nach unten
0 * DEG_TO_RAD,
angles);
std::cout << "X: " << pose[0] << '\n';
std::cout << "Y: " << pose[1] << '\n';MRC - der MicroPede Robot Controller
Warum ein eigener Controller? MRC ist eine einfache, modulare, Mikrocontroller-basierte Robotersteuerung. Ziel war es, ein überschaubares System zu schaffen, dass sowohl intern, als auch an Schnittstellen erweiterbar ist.
Warum kein ROS? ROS ist super! Wir haben selbst auch einige Anwendungen mit ROS implementiert. Der MRC soll jedoch eine schlanke alternative darstellen, der ohne Host allein auf dem Microcontroller ausgeführt wird. Der Code ist modular aufgebaut und ermöglicht es Interessierten, jedes Element der Robotersteuerung nachvollziehen und erweitern zu können.
Folgend sind die einzelnen Module des MRC dargestellt:
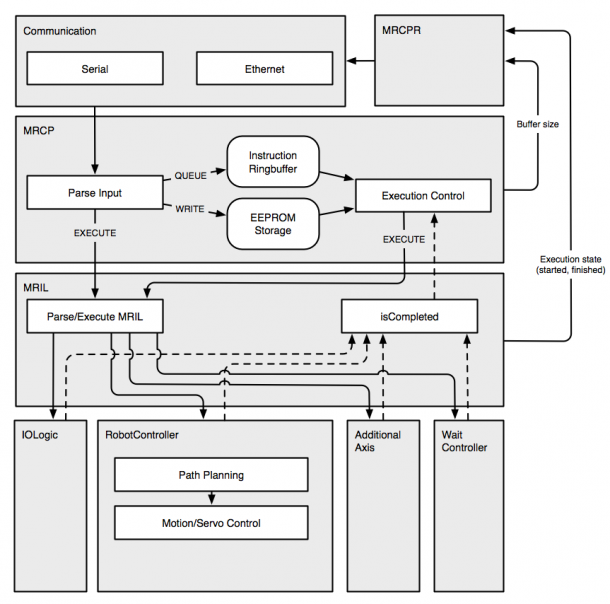 Eine genauere Beschreibung der einzelnen Komponenten bitte den jeweiligen Abschnitten entnehmen.
Die Kommunikation mit dem MRC erfolgt über eine Serielle-Schnittstelle. Weitere Kommunikationsarten, wie TCP über Ethernet sind zudem möglich, jedoch noch nicht implementiert.
Das Modul MRCP (gleichnahmig zum MRCP-Protokol, siehe Abschnitt MRCP) verarbeitet die eintreffenden Daten und speichert die Anweisungen in Puffern, EEPROM, oder führt diese direkt aus.
Interpretiert und ausgeführt werden die Anweisungen im Modul MRIL. Hier werden die einzelnen Befehle ausgewertet und an die Aktiven Module
(IOLogic - Steuerung ein und Ausgänge; RobotController - Bewegungssteuerung; AdditionalAxisController - Zusätzliche Achsen, wie Greifer; Wait Controller - Warteanweisungen).
Zudem erfragt das Modul MRIL von den Aktivkomponenten den aktuellen Status. Haben alle Komponenten ihre Verarbeitung abgeschlossen,
so lädt die Execution Control des MRCP die nächste Anweisung aus dem Speicher/Puffer.
Eine genauere Beschreibung der einzelnen Komponenten bitte den jeweiligen Abschnitten entnehmen.
Die Kommunikation mit dem MRC erfolgt über eine Serielle-Schnittstelle. Weitere Kommunikationsarten, wie TCP über Ethernet sind zudem möglich, jedoch noch nicht implementiert.
Das Modul MRCP (gleichnahmig zum MRCP-Protokol, siehe Abschnitt MRCP) verarbeitet die eintreffenden Daten und speichert die Anweisungen in Puffern, EEPROM, oder führt diese direkt aus.
Interpretiert und ausgeführt werden die Anweisungen im Modul MRIL. Hier werden die einzelnen Befehle ausgewertet und an die Aktiven Module
(IOLogic - Steuerung ein und Ausgänge; RobotController - Bewegungssteuerung; AdditionalAxisController - Zusätzliche Achsen, wie Greifer; Wait Controller - Warteanweisungen).
Zudem erfragt das Modul MRIL von den Aktivkomponenten den aktuellen Status. Haben alle Komponenten ihre Verarbeitung abgeschlossen,
so lädt die Execution Control des MRCP die nächste Anweisung aus dem Speicher/Puffer.
Die Komponenten
Neben dem MRC gibt es noch weitere Komponenten und Werkzeuge, die das Arbeiten mit dem Roboter ermöglichen.
MRIL - Micropede Robot Instruction Language
Gesteuert wird der MRC mit Hilfe der MRIL. Die MRIL ist eine an G-Code angelehnte, textbasierte Anweisungs-Sprache.
Ziel war es, einen einfachen, logischen textbasierten Anweisungssatz zu definieren, der textuell geschrieben und beispielsweise mittels
screen über "USB" seriell versendet werden kann.
Eine Anweisung besteht jeweils aus einer Zeile (mit \n terminiert) und ist wie folgt aufgebaut:
[{instruction number}]{command}[{command}...]
^optionale Anweisungsnummer ^1..n BefehleEin Befehl besteht aus Symbol XYZABCDWIOM (schreibungsunabhängig), optionalem Selektor 0..9 und einem Wert 0..n. Leerzeichen werden ignoriert
und dienen lediglich der besseren Lesbarkeit.
| char | command | syntax | example | description |
|---|---|---|---|---|
| M | movement method | M{method:00/01/02} | M00 | 00 - P2P; 01 - Linear; 02 - Circular |
| V | velocity | V{velocity:0-999} | V100 | Sets linear or angular velocity based on M command! (if M00 V == time) |
| X | x coordinate | X{coordinate:±0-999} | X 0 | |
| Y | y coordinate | Y{coordinate:±0-999} | Y -12.3 | |
| Z | z coordinate | Z{coordinate:±0-999} | Z 0.5 | |
| A | euler angle a | A{angle(deg):±0-360} | A270 | Euler in X->Y->Z rotation order, moving axis. |
| B | euler angle b | B{angle(deg):±0-360} | B180 | |
| C | euler angle c | C{angle(deg):±0-360} | C55 | |
| R | axis rotation | R{joint:0-9}{rot(deg):{±0-360} | R2 90 R7 0 | set target rotation. Additional axis (6-9) may be used |
| T | anchor circ. move | T{axis:0-2}{coordinate:±0-999} | T0 2 T1 5 T2 -5 | set anchor point for circular movement interpolation |
Eine vollständige Liste der Anweisungen findet sich auf GitHub.
Ein paar Beispiele zur Bewegungssteuerung:
M01 X15 Y-10 Z3 A0 B180 C0 # lineare Bewegung (M01) zu {15,-10,3,0,180,0}
M00 X20 # Point2Point-Bewegung zu {20,-10,3,0,180,0}
V3 X15 # Point2Point-Bewegung zu {15,-10,3,0,180,0} in 3s
R0 50 R1 20 R2 0 R3 30 # Achse 0 auf 50°, Achse 1 auf 20°, usw
R6 90 R7 30 # zusätzliche Achse 6 und 7 bewegen (z.B. Greifer)Einfache Logik- und Warteanweisungen sind ebenfalls möglich:
D3000 # warte (delay) 3000ms (3s)
I5 1 I6 0 # warte bis gleichzeitig Eingang 5 HIGH und Eingang 6 LOW ist
O4 0 # setze Ausgang 4 auf LOW
D1000 X-3 # fahre zu X-3 warte 1sAnweisungen werden stets komplett analysiert und ausgeführt. Die Reihenfolge der Befehle ist nicht relevant. Befehle mit
Bedingungen (warten auf IO, Zeit) werden als letztes ausgeführt, verzögern also die Ausführung der nächsten Anweisung.
So wird im Beispiel oben zunächst nach X-3 verfahren, dann 1s gewartet. Anweisungen sind zustandsabhängig.
Dass heißt, es müssen nicht bei jeder Anweisung alle Parameter angegeben werden. Einmal gesetzte und nicht geänderte
Befehle, wie Geschwindigkeit, werden für alle weiteren Anweisungen übernommen. Um deterministische und
portable Anweisungen zu erstellen, hat es sich bewährt, stets den kompletten Befehlsatz für eine Sollposition
anzugeben, damit Unbakannte aus vorherigen Anweisungen vermieden werden können.
Ein kleines Steuerungsprogramm, welches eine Kiste auf ein Förderband ablegt und aufnimmt:
M00 V20 O1 0 # P2P, Geschwindigkeit, Ausgang auf 0 setzten
X15 Y0 Z20 A0 B180 C0 # fahren in home position
M01 # linear
X15 Y-15 Z20 A0 B180 C0 # Aufnahmeposition
I0 1 # warten auf Signal von Förderband (Kiste bereit)
V1 R6 1 # öffnen Greifer (je nach kalibrierung 0:zu, 1:auf)
V5 Z15 # langsames senken über Kiste
V1 R6 0 # schließen Greifer
V10 Z20 # anheben
O1 1 # signal an Förderband (Kisten entnommen)
Y15 # Ablageposition
V5 Z15 # senken
V1 R6 1 # öffnen
V5 Z20 # hochfahrenMRCP - Control Protocol
Das MRCP wird zur Übertragung und Ausführung von MRIL Anweisungen verwendet. Eine Nachricht ist wie folgt aufgebaut:
[{start}][{execution mode}][{MRIL}]{end}
^Startsymbol ^Ausführungsmodus ^MRIL AnweisungDas Startsymbol : ist standardmäßig optional.
MRIL Anweisungen können auf drei verschiedene Arten am Controller ausgeführt werden.
- EXECUTE - Sofortiges Ausführen der Anweisung
- QUEUE - Schreiben der Anweisung in eine Warteschlange im RAM, die sukzesive abgearbeitet wird.
- WRITE - Speichern der Anweisung im EEPROM des Mikrocontrollers. Nach Erreichen der letzten Anweisung wird mit der Ersten fortgefahren.
Der Ausführungsmodus ist ebenfalls optional. Ist dieser nicht angegeben, wird die MRIL Anweisung
in die Warteschlange (QUEUE) geschrieben. Da sowohl Startsymbol, als auch Ausführungsmodus optionale Parameter darstellen,
können MRIL Anweisungen direkt an den MRC gesendet werden. So können die MRIL Anweisungen beispielsweise mit einem Seriellen-Monitor
oder screen händisch eingegeben und gesendet werden, ohne dass Startsymbole und Modi angegeben werden müsssen. X25 statt :Q X25.
MRCL - MicroPede Robot Control Library
MRCL ist eine NodeJs (JavaScript) basierte Bibliothek zum Erstellen und Senden von Anweisung an den MRC. Anweisungen werden an den Roboter über eine serielle Schnittstelle (USB) übertragen. (Die Steuerung ist durch andere Transportwege und Protokolle, wie TCP, erweiterbar). Eine Verbindung kann auf unixoiden Systemen beispielsweise mit dem Programm screen hergestellt werden. Um jedoch größere Programme zu übertragen und Anweisungen dynamisch an den Roboter zu senden, ist eine Programmschnittstelle sinnvoll.
Mit Hilfe der MRCL können Anweisungen erstellt und an den MRC gesendet werden.
const transport = new SerialTransport({
port: '/dev/cu.usbmodem123',
bausRate: 9600,
})
const mrcl = new MRCL(transport)
const mril = new MRIL('M01 X15 Y-10 Z12 A0 B180 C0')
const cmd = new MRCP(protocol.MRCP.QUEUE, mril)
mrcl.send(cmd)Zudem kann mit MRCL der Ausführungsstatus den MRIL überwacht werden:
mril.on('executing', () => {
console.log(`executing ${mril.getInstruction()}`)
})
mril.on('executed', () => {
console.log(`${mril.getInstruction()} executed`)
})Werden mehrere Nachrichten an den QUEUE des MRC üertragen, überwacht die MRCL automatisch die freie Puffergröße am MRC und sendet neue Nachrichten erst, sobald genug Speicher frei ist.
Der MRIB - Instruction Builder ist teil der Control Library und kann zum programatischen Erstellen von Anweisungen verwendet werden:
const mrib = new MRIB(mrcl)
mrib.queue()
.setOutput(0, 1).setInput(3, 1)
.setVelocity(2).moveP2P(10, -12, 10, 0, 180, 0)
.setVelocity(5).moveLinear(22, 10, 10, 0, 180, 0)Modul Robot Controller
Das, in der Architekturdarstellung gezeigte, Modul Robot Controller umfasst die Berechnung von Bewegungspfaden, Geschwindigkeits-Steuerung und Ansteuerung der Servomotoren. Es stellt ein Modul des MRC dar, kann jedoch auch eigenständig genutzt werden. Ihm werden Zielpose, Achsstellungen, Bewegungsart (linear, P2P, circular) und Geschwindikeit übergeben. Die internen Mechanismen und Zustände zur Ansteuerung des Roboterarmes sind folgend dargestellt:
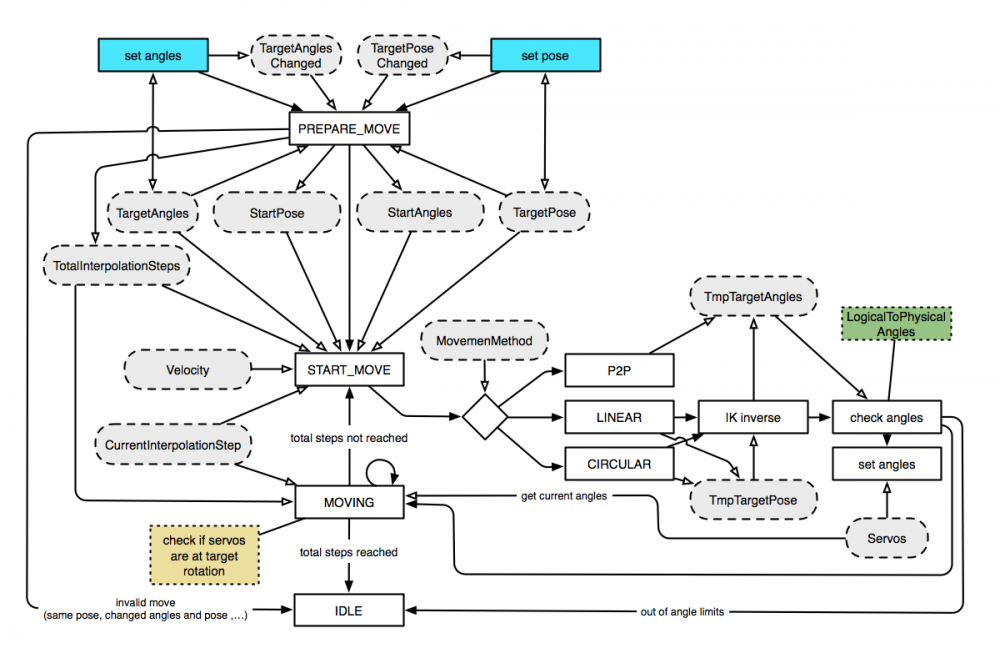
Teach-in - Achswinkel auslesen
Standard Hobby Servos erlauben es leider nicht die aktuelle Achsposition auszulesen, sondern lediglich die Zielposition vorzugeben. Eine Teach-in-Programmierung durch Führen des Roboters benötigt jedoch genau diese Informationen, um die Achswinkel zu speichern. Es besteht jedoch die Möglichket durch Modifikation der Motoren das interne Potentiometer auszulesen und dadurch die aktuelle Achsposition zu ermitteln. Hierfür muss meist nur ein Draht an das richtige Beinchen des Potenitiometers gelötet und nach aussen geführt werden. Anleitungen dazu finden sich im Web.
Inbetriebnahme
Um den Roboter in Betrieb nehmen zu können, sind folgende Schritte und Komponenten nötig.
- Roboter montieren (Werkzeug inklusive, benötigt wird zudem ein 3er Bohrer um den Kunststoffflansch aufzubohren, ein Kreuzschlitzschraubendreher und evtl. flüssige Schraubensicherung)
- Servos anschließen (Benötigt wird ein Netzteil 5-6V, 1-2A pro Servo -> min 6A.)
- Mikrocontroller (mit mindestens 6 PWM Ausgängen, oder Servo Steuerungsplatine)
- Servos kalibrieren - Relation zwischen Winkel und Pulsweite herstellen. Im Ordner examples auf GitHub findet sich dazu ein Skript (Video).
- Roboter steuern und helfen den Robotercontroller auf GitHub, gemäß des OpenSource Gedankens, zu verbessern :)
Servomotoren
Anschluss und Leistungsaufnahme
Ein Motor wird über die drei Leitungen V+ (rot), GND (braun), PWM (orange) mittels weiblichem Graupner-Stecker angeschlossen. Die Stromversorgung darf dabei nicht über den Microkontroller, sonder über ein dediziertes Netzteil geschehen.
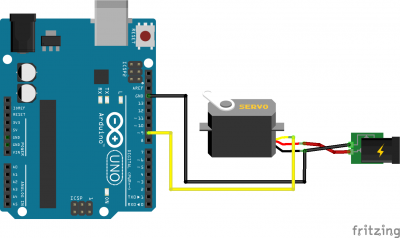
Als Richtwert können 1-2A Strombedarf pro Servo angenommen werden. Für einen 6-Achs Roboter wird folglich ein 6-12A Netzteil benötigt.
Ansteuerung
Angesteuert werden die Servos mit Hilfe von Pulsweitenmodulation (PWM). Dabei werden Pulse, definierter Länge, mit 50Hz (Periode: 20ms) an die im Servo eingebaute Elektronik gesendet und von dieser in Achswinkel umgesetzt. Die Servos nehmen meist Pulse im Bereich von 500μs-2000μs an und setzten diese in Winkel um. Der genaue Arbeitsbereich kann dem jeweiligen Servo-Datenblatt entnommen werden. Die Winkelgenauigkeit kann mit Hilfe der Angabe zum Totbereich (deadband) berechnet werden. Bei 2μs Totbereich, 180° Drehbereich und 500-1500μs PWM-Bereich ergeben sich 180/(1500-500)*2 = 0.36° Winkelgenauigkeit. Pulseänderungen unter 2μs können also vom Servotreiber nicht in Winkeländerungen umgesetzt werden. Zu beachten ist außerdem, dass es sich hierbei um einen theoretischen Wert handelt, der unter Last größer ausfallen kann. Die Pulse können beispielsweise mit einem Mikrocontoller, Arduino, Teensy oder RaspberryPi erzeugt werden.
Die Abbildung von Steuerpulsen auf Achswinkel ist nicht bei allen Servotypen deterministisch. Das heisst, dass verschiedene Servos
bei der selben Pulslänge nicht unbedingt die selben Winkelstellung einnehmen. Es empfielt sich daher,
eine einfache Konfiguration vorzunehmen, in welcher der Motor mit bestimmten Pulsweiten angesteuert und der wahre Achswinkel
mit Hilfe eines messenden Verfahrens bestimmt wird. Mit der Funktion pw = map(targetAngle, minAngle, maxAngle, minPW, maxPW)
kann dann die Pulsweite unter Verwendung der gemessenen Winkel und Pulsweiten bestimmt werden.
Servos zittern, brummen
Ein Servozittern ist meist auf Störungen im PWM Signal bzw. Schwankungen in der Spannungsversorgung zurückzuführen. Es können sog. Ferritkerne/ringe zur Entstörung eingesetzt werden. Das Servokabel wird dazu um den hochinduktiven Kern gewickelt. Das System wirkt als Spule und entstört so das Steuersignal. Sollten die Servos zittern, sobald sie oder andere Servos in Bewegung sind, ist dies meist auf ein unterdimensioniertes Netzteil zurückzuführen. Hier können Kondensatoren zum Abfangen von Strombedarfsspitzen eingesetzt werden.
Ein Servobrummen unter Last ist üblich, da die interne Servosteuerung versucht gegen die Last zu arbeiten und dadurch diesen stetig ansteuert. Da die Motoren nicht über ein selbsthemmendes Getriebe verfügen, muss auch bei Stillstand geregelt werden. Auch das Eigengewicht des Roboterarms kann ein Brummen auslösen.